엔트로피의 정의와 인공지능의 요구

'엔트로피'라는 단어는 1865년 독일의 물리학자 루돌프 클라우지우스가 처음으로 사용했다. 엔트로피라는 단어는 에너지라는 뜻의 그리스 어원에서 출발했다. 엔트로피는 일반적으로 무질서도라고 알려져 있기도 하며, 미시적 상태의 무질서한 정도를 표현한다.

그런데 열역학 제2법칙에서는 항상 전체 계(System)의 엔트로피가 증가하는 방향으로 사건이 일어난다고 한다. 이 법칙에 따르면 시스템은 엔트로피가 증가하는 쪽으로, 즉 무질서해지는 쪽으로 변하려 한다고 한다. 그래서 전 우주에서 부분으로 뭉쳐있는 에너지가 전체에 걸쳐 평평하게 흩어져가는 과정이 엔트로피의 증가과정이라고 본다. 즉, 엔트로피의 증가는 평형 상태로의 이동이며 에너지적으로 볼 때는 안정화되는 방향이다.

그런데 반대로 인공지능에서는 엔트로피가 감소하는 방향으로 학습을 최적화하기도 한다. 물리 법칙과 인공지능이 반대인 경우이다.

한편, 전자공학의 한 학문 분야인 ‘정보 공학’ 분야에서도 엔트로피 개념이 사용된다. 특히 인공지능과 관련해 정보 이론을 이용해서 인공지능 네트워크를 최적화하고, 그 이론을 뒷받침하려는 연구가 있다. 이러한 새로운 시도는 정보 이론 수학과 인공지능의 만남이다. 엔트로피로 대표되는 정보공학 이론이 인공지능 발전에 어떠한 기여를 할지 미래가 궁금하다.

정보 이론에서 정보의 양을 지수 I로 표현한다. 어떤 일이 일어날 확률을 P(x)라고 할 때, 그것이 갖는 정보량은 I=-Log2(P(x))로 표현된다. 정보를 확률의 로그 함수로 표현한다. 예를 들어 확률이 50%인 P(x)=1/2=0.5라고 하면 정보량 I=-Log2(1/2)=1이 되어 I=1이 된다. 그 뜻은 그 정보를 1비트의 2진수로 표현할 수 있다는 뜻이 된다.

이러한 정의와 수식에 따라 확률이 낮을수록 정보량이 커진다. 거꾸로 확률이 높으면 정보량이 적어진다. 이 같은 확률에는 학교 성적 분포를 예로 들 수 있다. 학교 성적이 넓게 골고루 퍼져 있으면 정보량(I)이 많다. 점수가 골고루 분포돼야 학생의 능력을 구별하기 쉽고, 성적 주기도 편하다.

반면에 높은 성적과 낮은 그룹이 확 구별되면 성적이 특정 점수대에 몰려 있게 된다. 이때 정보량이 낮다. 학점은 2개 종류밖에 없게 된다.

여기에 더 나아가 정보 이론에서는 엔트로피(Entropy)가 정의된다. 엔트로피는 정보량과 확률 곱의 결과물이다. 정보량과 마찬가지로 넓게 골고루 분포하면 엔트로피가 높고, 특정 지점에 확률이 몰려있으면 엔트로피가 낮다.

예를 들어 주사위의 경우, 모두 6개의 면이 나올 확률이 1/6이다. 그래서 확률이 넓게 퍼져있다. 이 경우 엔트로피가 높다. 반면 윷놀이는 도(4/16), 개(6/16), 걸(4/16), 윷(1/16), 모(1/16)가 나올 확률이 각각 다르다. 분포가 균등하지 않다. 결국 윷놀이의 엔트로피가 낮다. 각각 확률의 차이가 크기 때문이다.

이러한 개념의 엔트로피가 인공지능에도 그대로 사용된다. 인공지능에서는 결과가 잘 구별되도록 엔트로피를 낮게 최적화한다. 인공지능에서는 주사위보다는 윷놀이를 원한다.

인공지능에서 출력 결과 값이 분명할수록 좋다. 그래야 인공지능이 미래를 명확하게 판단할 수 있고 미래를 예측한다. 알파고가 게임을 할 때도 인공지능이 이길 승률이 가장 높은 수를 명확히 알려 주어야 한다. 그래서 인공지능의 출력의 확률 분포는 엔트로피가 낮을수록 좋다고 볼 수 있다. 인공지능은 엔트로피 작은 방향을 선호한다.

인공지능에서 사용되는 엔트로피 비용함수

인공지능인 딥 뉴럴 네트워크(Deep Neural Network, DNN)는 대표적으로 두 종류로 나누어진다. 이미 정답을 알고 있고, 그 정답을 이용해서 인공지능을 교육하는 지도학습 (Supervised Learning)과 정답 없이 인공지능 스스로 학습하는 비지도 학습(Unsupervised Learning)으로 나누어진다.

지도 학습의 경우, 입력 데이터를 넣고, 인공지능 예측 결과를 얻는다. 예를 들어 사진을 입력으로 넣고, 고양이인지 호랑이인지 판독한다. 이때 주어진 정답과 인공지능 출력이 같을 수도 있고, 다를 수도 있다. 이때 정답과 인공지능 출력, 두 개의 차이를 함수로 정의하는 데 이를 수학적으로 비용함수(Cost Function)라고 한다.

이 비용함수를 최소화하기 위해서 인공지능 네트워크 변수들을 정해간다. 이를 학습(Training)이라고 부른다. 비용 함수의 선택에 따라 학습의 속도, 정확성에 차이가 난다.

가장 이해하기 쉽고 많이 쓰이는 비용함수가 제곱 오차 함수(Mean Square Error, MSE)이다. 즉, 정답과 인공지능 결과의 차이를 제곱해서 모두 더하는 것이다. 그래서 두 차이가 클수록 비용함수 값이 커진다. 최종 학습 결과로 비용함수가 ‘0’이 되면 제일 좋다. 그때 이 비용 함수의 미분도 ‘0’이 된다. 이처럼 비용함수가 최소화할 때까지 학습을 계속해 간다.

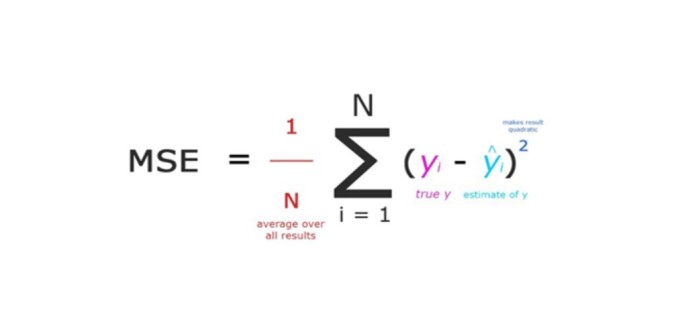
그런데 또 다른 매우 용한 비용함수가 정보 이론에서 제시하는 엔트로피 함수이다. 엔트로피 함수를 사용하면 학습이 좀 더 빠르다. 다른 말로 혼란을 최소화하고, 분명한 결과를 내려면 엔트로피 값이 최소화된다.

이처럼 엔트로피 개념과 함수가 인공지능에서 유용하게 사용된다.

우리가 사는 세상의 엔트로피

인간 사회도 정보이론의 엔트로피로 표현할 수 있다. 다이내믹 코리아(Dynamic Korea)로 표현되는 우리 사회는 엔트로피가 높다고 할 수 있다. 에너지가 넘치고, 그 결과, 시간이 지나면 사회가 평형을 이룬다.

이렇게 엔트로피가 증가하는 방향은 사회 전체가 평등하다고 볼 수 있다. 사회의 자본, 정보 그리고 기회가 이렇게 골고루 퍼지면 좋다. 또한 누구나 열심히 일하면 계층이동을 할 수 있다. 이런 사회가 엔트로피가 높다.

반면에 사회의 자본, 정보 그리고 기회를 소수가 독점된 사회는 엔트로피가 낮다. 빈부격차가 큰 사회는 엔트로피가 낮다. 좌우 갈등이 높으면 엔트로피가 낮다.

인공지능은 빠르고 냉철한 지능을 가지려고 엔트로피가 낮은 방향으로 학습한다. 그렇게 보면 인공지능은 효율적이지만 냉정한 지능이다. 따뜻한 가슴이 없다.

[김정호 카이스트 전기 및 전자공학과 교수] joungho@kaist.ac.kr